Van der Waals and Nitrox

Who was Van der Waals anyway and what has he to do with my Nitrox fill?
Revised Version
Full screen

JOHANNES DIDERIK VAN DER WAALS 1837-1923 Amsterdam University
1910 Nobel Prize for Physics for his work on the equation of state for gases and liquids.

This tends to indicate that he knew his stuff.

OK. The simple rules for gases about pressure, volume and temperature that you learnt in Scuba for beginners are only an approximation. Good enough for some poor lad or lass who has to worry about doing a mask clear without a total sinus washout but now you've grown up and want to breathe fancy stuff it just won't cut it anymore.

You haven't forgotten but we'll recap anyway.
Do you remember PV=kT?
The ideal gas law? Oh yes. The one that summarised all the others ones that we can't remember the names of. We usually think of it as PV = quantity of gas. That's the one. Well let us get rid of that nasty k for an arbitrary constant and turn it into the real one PV=nRT that scientists and engineers use. This is much better because we can calculate real things with it rather than just do ratios. Let's name the parts in useful units:

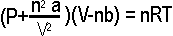
P	Pressure in bar
V	Volume in Litres
n	Quantity of gas in mols
R	The universal gas constant, which is 0.0831451 if we want to do bar and litres
T	The temperature in Kelvins (virtually Centigrade+273)

mols? Well it's a chemist's trick to have a measure of something rather than work in boring units like grams.
A mol is a gram molecule. It is the amount of a substance that weighs X grams where X is the molecular weight of the molecule in question.
For example Oxygen has an atomic weight of 16 (well 15.994 if you want to get all isotopic about it) so O2 has a molecular weight of 32. Hence 32 grams of O2 is one mol and 64 grams is 2 mols etc. Plutonium Oxide has a molecular weight of 536 so it takes over half a kilo of that stuff to make a mol but chemists don't care. The neat trick is that 1 mol contains 6.02x1023 molecules. A mol is not so much a quantity as a head count and is great when you are working out how things react.

Great. Real numbers. Let's do an example. The 100% oxygen deco bottle is 3L, it is January at Stoney Cove so it is 4°C, that is 277K and we want the whole 300 bar.
So n = PV/RT so n = (fumbles with calculator) n = 39 mols so at 32 grams to the mol we have 1.248 Kilograms of Oxygen.

Then along comes Van der Waals in spoil sport mode and says "well not really".

The trouble is that this thing is the Ideal gas law. That is it only really would work for an ideal gas and all we have are real ones. An ideal gas would be composed of infinitely small molecules that did not attract one another but real gases have real sized molecules taking up the space and they tend to attract and repel one another. Van der Waals was the man who set about solving the problem by working out how to allow for real gases.

What he came up with was not the exact answer but a much better gas equation.

If you look at it and remember PV=nRT you can see the old ideal gas equation in here but with two extra terms, one applying a fiddle factor to the pressure to allow for the attraction between molecules drawing them inwards and increasing the effective pressure and the other fiddle factor is on the volume where it is effectively reduced to allow for the fact that all these molecules are taking up the space.
We get two new constants a and b which depend on the gas we are considering.

Back to the example for our tank of O2 and use the Oxygen a value of 1.382 and the b value of 0.03186 and we get a different situation.
Putting our 1.248Kgs, ie. our 39 mols of Oxygen into our 3L tank, gives 277bar.

OK let's graph that with mols (quantity) along the bottom and pressure in bar up the left.

What's this mean? The nice straight purple line is gas pressure against mols of gas for the Ideal law. The blue line curving upwards is Van der Waals' calculation.
Down at 0 to 20 bar, where you did you school physics and do your diving it is very good. Up at 100 bar it takes 15 mols of Oxygen to get to 100 bar and you can see the modified P term compensating for the molecules attracting one another and pulling inwards so reducing the pressure they apply to the outside world. At 200 bar it takes 30 mols and the line is begining to turn back as the modified V term compensates for the size of the molecules taking up the free space and finally at 300 bar you do not have the 45 mols you were expecting but just 41. This is why divers get edgy about mixing Nitrox to 300 bar final pressure because the pressure is no-longer an exact equivalent to quantity. 150bar of Oxygen then 150bar of Nitrogen is not a 50% mix anymore.

It gets worse.
We assume for ideal gases that we can work out the partial pressures independently and just add them up (Dalton's Law) and moreover we assume that the ratios don't change with pressure. Now for nitrox it happens that the a and b values for Nitrogen are very similar to Oxygen but if (simplistically) we put 100 bar of Oxygen in a tank and then topped it off to 300 bar with pure Nitrogen we do not have 33% Nitrox. It is a bit higher. More like 37%.

We can calculate it but Van der Waals' equation as stated above only applies to the simple monatomic gases and as the molecules of one gas see the others nothing is simple. However we can produce modified a and b constants for the mixed gas formed using the values for each gas combined using:

What on Earth? Yes. I did university physics and I winced a bit at that one. What it is saying that for a mixed gas made of n gases (1 to n) whose fractions (ratio of mols) are x1, x2, x3... xn and whose a and b values are a1, b1, a2, b2 etc. then you get the global a and b values by taking the formula to the right of the two sigma signs and adding up all the bits. If you have three gases (Oxygen, Nitrogen and Helium for example) then

a = √(a1*a1)*x1*x1 + √(a1*a2)*x1*x2 + √(a1*a3)*x1*x3
+ √(a2*a1)*x2*x1 + √(a2*a2)*x2*x2 + √(a2*a3)*x2*x3
+ √(a3*a1)*x3*x1 + √(a3*a2)*x3*x2 + √(a3*a3)*x3*x3

and naturally b looks much the same. This was probably grief to poor old Van der Waals but we have spread-sheets on our home computers...
Once you have done this you can work out the total pressure but don't think in partial pressures, Dalton style, any more because they don't exist. Definitely don't try to work back from pressure to ratio. It's horrible.

If you want to do a Trimix calculation then first you need to generate some real a and b values so here are a and b for the three gases we tend to worry about so you don't have to buy the great big book I did.

	a	b	mw
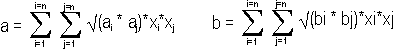
Oxygen	1.382	0.03186	31.9988
Nitrogen	1.370	0.03870	28.01348
Helium	0.0346	0.02380	4.0020602
Air (treat as)	1.3725	0.0372	28.85

Bit esoteric eh?
Try this one then.
My twins contain 20L at 300 bar
I want to get out of two dives with the equivalent of 50bar in my one old 12L reserve
I want to do two dives so what is half way?
Twins at 20L at 300bar is 226 mols
12L at 50bar is 25 mols
25 mols in the twins is 30bar so I can breathe 201 mols
So half way down is, say, 100mols breathed 126 mols left
126 mols in the twins is 146bar
The ideal gas law would have said half way was (300-30)/2+30 = 165bar so I would have called time early on the first dive and probably wondered why my buddy, on two single 12s - one for each dive, called time on the second.

You don't want to do maths?
OK so you don't want to do the sums you want the tool to do the sums for you.
Right. Here is the blender program for both desktop Windows and an iPaq running Pocket PC available from the main index .

One last thing.
It is the partial pressure of the mix at 1 to 10 bar that we breathe and so what we measure on our Oxygen analysers is what we get. You do not have to worry that the stuff in the tank is not going to be what you measure or that the mix will change as the absolute pressure in the tank changes. The ratio of the number of gas molecules is what you care about so if it measures 38% it will stay 38%. The pressure may drop a little quickly to start with because that 200-300 bar slice of the fill was only 84% of the 0-100 or 100-200 parts of the fill.

Back to the index